2025年度(令和6年度)の福岡県公立入試数学予想問題と解説についての記事です。大問1番については、志望校がどこに限らず全問正解が必須の大事な問題となります。本番を想定して、大問1~大問6まであります。
数学の予想問題(福岡県公立高校入試)
<大問1>
次の(1)~(9)について、( )の中にあてはまる最も簡単な数または式を記入せよ。ただし、根号を使う場合は√の中を最も小さい整数にすること。
(1)2-3×(+4)=( )
(2)2(a-1)-(3a-4)=( )
(3)a=5,b=2のとき、-a+3b2の値は( )である。
(4)√20-5√5=( )
(5)1次方程式2x-9=x+3を解くとx=( )である。
(6)2次方程式x(x+5)=2(x+9)を解くとx=( ),( )である。
(7)yはxに反比例し、x=4のときy=3である。x=-6のときのyの値は、( )である。
(8)4枚の硬貨A,B,C,Dを同時に投げるとき、1枚が表で3枚が裏である確率は、( )である。ただし、どの硬貨の表裏が出ることは同様に確からしいものとする。
(9)水そうに、赤い金魚が多くいる。赤い金魚の数を調べるために、黒い金魚100匹を水そうに入れ、その中から60匹の金魚を無作為に抽出し、黒い金魚の数を調べた後、抽出した60匹の金魚をすべてもとの水そうにもどす。これを繰り返しおこなったところ、黒い金魚の平均は、1回あたり12匹であった。このとき、水そうにいる赤い金魚は、約( )匹と推定できる。
<大問2>
はるかさんとたけるくんは、トレーナーとTシャツを買いに、カジュアルファッションショップへ行った。この店ではトレーナー1枚x円、Tシャツ1枚y円の定価がついている。次の会話を読んで、問いに答えなさい。
| 会話 | 内容 |
|---|---|
| 店 長 | 今日は「福岡一人一花サイコロ割引セール」を実施しています。代金を支払うとき,大小2つのサイコロを投げてください。割引率は2つのサイコロのそれぞれのでた目の積で決めます。例えば、2と5が出たら,2×5で定価の10%を割り引きます。6と6が出たら、6×6で定価の36%を割り引くことになります。なお,消費税はサービスとしていただきません。 |
| はるか | トレーナー1枚とTシャツ3枚を買います。 |
| 店 長 | では、2つのサイコロを投げてください。 |
| はるか | 2と6が出ました! |
| 店 長 | 2×6だから定価の12%を割り引いて,代金は7040円になります。 |
| たける | トレーナー2枚とTシャツ1枚を買います。 |
| 店 長 | では、2つのサイコロを投げてください。 |
| たける | 5と4です。 |
| 店 長 | 5と4だと、割り引いて、代金は9600円ですね。 |
トレーナー1枚x円、Tシャツ1枚y円として、連立方程式を完成させ、それぞれの定価を求めなさい。なお、求めるまでの過程も示しなさい。
<大問3>
2けたの整数は、十の位の数をa, 一の位の数をbとすると、10a+bと表すことができます。これを利用して、「2けたの整数と、その数の十の位の数と一の位の数を入れかえた整数との平方の差は、99の倍数である」ことを証明しなさい。
<大問4>
図1のように、200L の水が入る水そうがあります。この水そうには給水管 A, B がついており, 最初はA管だけで10分間給水します。次に A 管を閉じ、その5分後にA, B両管を使い, 満水になるまで給水します。図2は,水を入れ始めてからx分後の水の量をyLとしたとき, 満水になるまでの x, y の関係をグラフに表したものです。このとき, 次の問いに答えなさい。
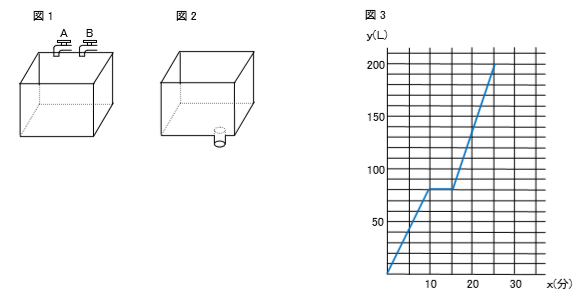
(1) 給水管 A では, 毎分何 L の割合で給水しましたか。
(2) 給水管 A, B の両管で給水したときの xとyの関係を式に表しなさい。また, xの変域も答えなさい。
(3) 図2の水そうも, 図 1 の水そうと同じ大きさで 200L の水が入り, 満水の状態になっています。 この水そうには配水管がついており, 図 1 の水そうに給水を始めるのと同時に, 毎分 6L の割合で排水します。このとき、2つの水そうの水の量が等しくなるのは, 排水を始めてから何分後か求めなさい。
<大問5>
図のように、△ABC とその辺 BC を直径とする円がある。この円と辺 AB,辺 AC とは、それぞれ点 D,E で交わっていて、AD=1cm、DB=AC=2cmである。CD と BE の交点を F とするとき、次の問いに答えよ。
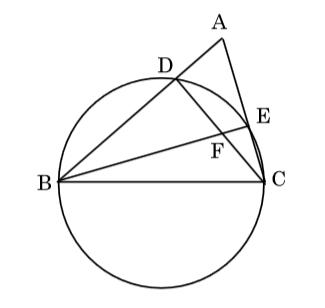
(1)△ACD∽△FBD を証明せよ。
(2)CD の長さを求めよ。
(3)BE の長さを求めよ。
(4)△BCF の面積を求めよ。
<大問6>
下の図のように、底面の半径=5cmの円すいがある。母線OA上にPをとり、OPの長さが12cmで、PからOB上に下ろした垂線PCの長さが2cmである。次の問いに答えなさい。
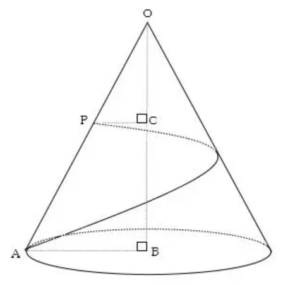
(1)OCの長さを求めなさい。
(2)APの長さを求めなさい。
(3)円すいの表面積を求めなさい。
(4)下の図のように、Aから側面上に回ってPまでいく最短距離を求めなさい。
数学の予想問題(福岡県公立高校入試)の解答
<大問1>
(1)-10
(2)-a+2
(3)7
(4)-3√5
(5)12
(6)3,6
(7)-2
(8)1/4
(9)400
<大問2>
0.88(x+3y)=7040
0.8(2x+y)=9600
これを解くと、x=5600 y=800
これは問題にあう
トレーナー5600円、Tシャツ800円
<大問3>
入れかえた2けたの整数は、10b+aと表せるので
(10a+b)2-(10b+a)2
=100a2+20ab+b2-(100b2+20ab+a2)
=99a2-99b2
=99(a2-b2)
ここで、(a2-b2)は整数なので99(a2-b2)は99×(整数)となり、99の倍数となる。よって、2けたの整数と、その数の十の位の数と一の位の数を入れかえた整数との平方の差は、99の倍数である。
<大問4>
(1) グラフより 10 分間で 80L 給水しているから毎分の給水量は 8(L) である。
(2) グラフより 2 点(15,80), (25,200)を通る直線で, 変域は 15≦ x ≦25 。傾きは、yの増加量/xの増加量より、12。さらに、点(15,80)を通るから y=12x+bに代入して、80=12×15+b b=-100 よって、y=12x-100(15≦x≦25)
(3) 50/3 分後
<大問5>
(1)
△ACD と△FBD において
∠ACD=∠FDB=90°(直径BCの円周角)…①
∠ACD=∠FDB(弧DEの円周角)…②
①②より、2 組の角がそれぞれ等しいので、
△ACD∽△FBD
(2)求める線分CDは、△ADCに着目して三平方の定理。ここでは、△ADCは、特別な直角三角形(1:2:√3 )なので、CD= √3 cm
(3)3√3/2
(4)√3/3
<大問6>
(1)OC=2√35
△OPCで三平方の定理から、OC2=OP2-PC2となり、OC2=122-22 これを解いて、OC=2√35
(2)18cm
求めるAP=xcmとする。
PC:AB=OP:OA=2:5となり、OP:AP=2:3=12cm:xcm これを解くと、xcm=AP=18cmとなる。
(3)175πcm3
公式より、OA×AB×π+AB×AB×π=30×5×π+5×5×π=175πcm3
※円錐の側面積=母線×半径×π 円すいの底面積=半径×半径×π
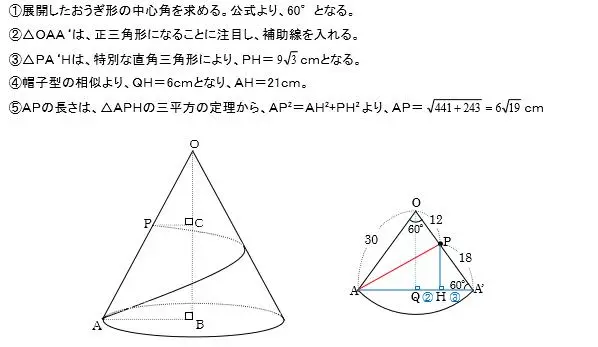
(4)6√19
展開したおうぎ形の中心角 母線×中心角=半径×360
| ▼ その他の科目 |
|---|
| 福岡県公立高校入試「国語」の出題予想 |
| 福岡県公立高校入試「理科出題予想と対策」 |
| 福岡県高校入試「社会」の傾向と対策 |
| 福岡県公立入試「英語大問5番(英作文)」予想問題 |

コメント